 The calculation of parameters from the stress-strain graph of a tensile test has already been covered in a previous blog post.
The calculation of parameters from the stress-strain graph of a tensile test has already been covered in a previous blog post. The calculations considered were those most often used when referring to stress and strain, and to give them their full name they would be called “engineering stress” and “engineering strain”. It is usually safe to assume that every time stress and strain are mentioned in the literature, this refers to the engineering values.
However, as the load on a sample increases, the cross-section over which the force is applied changes (it gets thinner). If the engineering stress is used (taking into account the initial area), the stress is underestimated. True stress solves this issue by using the instantaneous area over the course of application of load so that as the cross-section changes, the value of stress is calculated using the new cross-sectional area.
Additionally, whereas engineering strain is the amount that a material deforms per unit length, true strain is the natural log of the current length over the original length.
A true stress-true strain graph can be calculated from standard stress-strain data by the use of some conversion equations, making a few assumptions along the way. The test configuration is the same as for a normal tensile test. The following analysis calculates several useful parameters from a tensile true stress-true strain graph, using the standard equations for true stress and true strain of a beam undergoing tension. Depending on the nature of the sample it will show some or all of the characteristics of the stress-strain graph below. Different materials show very varied graph shapes.
There are many parameters that can be calculated from an ordinary stress-strain graph (such as Young’s modulus, yield stress and ultimate tensile strength). The graph of true stress – true strain is not generally used to find these parameters as true stress and engineering stress are often very similar up to the point of necking (as the cross-sectional area has not decreased by much). But true stress and strain are very useful for post-necking behaviour, especially for determining the onset of necking and the strain hardening parameter.
Calculating True Stress on a Texture Analyser
The equation for engineering (or “ordinary”) stress is:
And for true stress:
As it is very difficult to measure the changing cross-sectional area during a test, an estimation can be made. Assuming the material volume remains constant,
Rearranging the equation for true stress,
where ε is the strain, δ is the increase in length, L0 is the initial length and L is the new length.
and so the true stress axis is calculated as [engineering stress * (1 + strain)]
Calculating True Strain
As mentioned above, true strain is the natural log of the current length over the original length. True strain takes into account the path along which the final strain configuration is reached and is a more realistic way of calculating strain. To achieve this, the total deformation is divided into small sections. If dL is the change in length for each small section and L is the initial length of that section, then the strain over that section is:
and the total strain for a change of the sample from L0 to L is
which is the “true strain”. As
true strain ‘e’ and engineering strain ‘ε’ are related by the following equation
Using an Exponent Macro for a True Stress-Strain Graph
A macro has been set up to use these equations to plot a graph of true stress against true strain as shown below. In general, true stress and engineering stress graphs are almost equivalent up to yield, after which true stress is higher and they diverge, especially after necking.
The following graphs show stress and true stress with the equivalent strains.

From this graph, the onset of necking and strain hardening parameter can later be calculated according to the following diagram:
After yield, the true stress/strain curve can be approximated to the equation
Strain hardening parameter – the term ‘n’ in the equation above. This is a materials constant that represents the degree of work hardening a material undergoes during deformation. The value of the parameter is between 0 and 1. A value of 0 means the sample is perfectly plastic and a value of 1 means it is perfectly elastic.
Strength coefficient – the term ‘k’ in the equation above is known as the strength coefficient.
Strain at the onset of necking – this is the point of instability, when a neck forms and the cross-sectional area starts decreasing rapidly at one point. It occurs when the true strain is equal to the strain hardening parameter, when
Although the strain at necking and the strain hardening parameter are equivalent, one is often used in preference to the other.
The generation of a true stress-true strain graph and the use of its key parameters is an advanced form of analysis, but one that can be carried out quickly and easily by the use of an Exponent macro.
There is a Texture Analysis test for virtually any physical property. Contact Stable Micro Systems today to learn more about our full range of solutions.
For more information on how to measure texture, please visit the Texture Analysis Properties section on our website.
 The TA.XTplus texture analyser is part of a family of texture analysis instruments and equipment from Stable Micro Systems. An extensive portfolio of specialist attachments is
available to measure and analyse the textural properties of a huge range of
food products. Our technical experts
can also custom design instrument fixtures according to individual
specifications.
The TA.XTplus texture analyser is part of a family of texture analysis instruments and equipment from Stable Micro Systems. An extensive portfolio of specialist attachments is
available to measure and analyse the textural properties of a huge range of
food products. Our technical experts
can also custom design instrument fixtures according to individual
specifications.No-one understands texture analysis like we do!
To discuss your specific test requirements click here...
 |  |  |

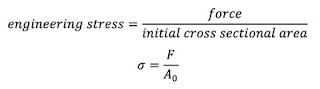











No comments:
Post a Comment